Robot Claw

This is one I’ve been thinking about for a while: how far can you see in a forest?

I’ve always been intrigued by the effect forests have on our vision. Even in forests where trees are far apart that you can’t touch two at a time, you usually can’t see too far. When Bernard and I went up to the Grand Canyon last year, the forests there are very light on underbrush and the trees have a decent distance between them and you still can’t see much further than a few dozen feet. When I was camping in January and I got up early and saw pademelons everywhere, I couldn’t see them beyond a few meters into the woods.

So I’ve been thinking, is there an equation that governs view distance in a forest? Which naturally led me to try and devise one myself.

Once you sit down and think about it, you find it’s a bit of an open-ended problem. So I decided to start by thinking about an easier problem, and then expanding from there. So consider this one:

“You stand somewhere on one side of a flat field, and your friend stands somewhere on the other side. The field is full of trees. What is the percent chance you can see your friend?“

This is not a brain teaser with an easy answer, and the result will depend on many things:
– Where you stand
– Where your friend stands
– The size of the field
– The number of trees
– The size of the tree trunks

Problems with many unknowns can get difficult to solve quickly, so the first step is to eliminate some. The first two (location of you and your friend) can be expressed as the distance between you and them. The last three (field size, tree count and tree size) can be expressed as a ‘wood density’ (ie. the total cross-sectional area of the trees divided by the area of the field).

I speculate the general solution is some function of the distance between you and them, and the wood density. But how does one calculate the result?

As I teach my students, always approach a problem from extremes. The two extremes here are easy:
– If the wood density is zero (there are no trees) the chance you can see your friend is 100%
– If the wood density is 100 (the field is chock-a-block with trees) the chance you can see your friend is 0%

So we expect an answer somewhere between 0 and 100%. This may seem trivial, but there are problems in which the percent range can be much tighter and it’s useful to know we have the full 100%.

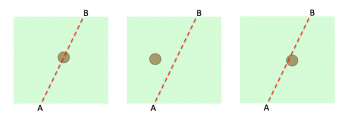
But what if there is only one tree? Consider these possibilities:

On the left you (A) can’t see your friend (B) because a tree is smack in the middle. In the middle you can (the tree doesn’t block your view), but on the right you can’t either because the tree just blocks your view. Any general solution must account for all such possibilities (and an infinite amount more).

So how to calculate a percent chance for one tree? There is no way I can surmise to solve this via a general equation solution, so the required tool is computer simulation, specifically Monte Carlo simulation. In essence: generate a very large amount of ‘maps’ (of you, your friend and one tree) and calculate the percent chance from solving each and adding them.

For instance, if the only possible configurations were those shown above, the chance of seeing your friend would be 33.3% (only one in three maps). Of course there are many, many maps though (as many as you want actually), and it would be impossible to solve them all, so a more rigorous method is needed.

Here’s how I would do it – and I welcome any theorists to give their techniques in the comments. This is (at this point), for one tree only:

1) Randomly generate your position (A) on the edge of the field
2) Randomly generate the position of your friend (B)
3) Determine the vector connecting the two of you (AB)
4) Randomly determine the position of the tree
5) Determine if the vector between A and B is blocked by the tree

This last step is trickier than it sounds, and the easiest way to do it (aside from a clever technique I discuss below*) might be to:
5a) Calculate the vector passing through the center of the tree perpendicular to the vector AB (this just requires some vector algebra)
5b) Calculate the intersection of these two vectors (more vector algebra)
5c) Calculate the distance between the point of intersection and the center of the tree (easy)
5d) If this distance is less than the tree radius, line-of-sight is blocked

The simulation would repeat the above steps many (n) times, incrementing a counter (p) by 1 every time you could see your friend. The final result would simply be (p/n)*100%

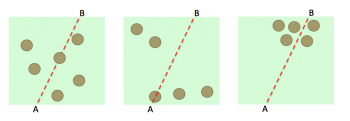
I imagine with only one tree the percent chance would be very high. But what about many trees?

That’s only 3 possible examples (from a pool of infinity) of five trees (well, six on the left!). You can see how much more complex the problem seems to become.

Interesting though, the simulation wouldn’t change much. The only difference would be to step 4 above, which would become:
4) Randomly populate the field with trees, saving their positions in an array

And then step 5 would be repeated for every tree. You wouldn’t have to test every single tree against line-of-sight for each AB vector, you could just stop when one blocked the view.

With this modified algorithm, I’d save (into my output file) the following:
1) Position of you (A)
2) Position of friend (B)
3) Size of field
4) # of trees
5) % chance of seeing friend (output of simulation)

Tests would have to be run to find out how many times the simulation needed to be ran. One thing I learned writing my simulation for my PhD was how few runs were actually necessary. My code would have happily ran all day long simulating billions of photos (each of which required hundreds of calculations) but in the end I stopped at only 1000. I found that the variability of the results for photon counts above 1000 was essentially 0, so there was no need to run more. It would be interesting to do the above coding and plot the results vs ‘maps’ ran and see where the plot gets flat. I bet it’s lower than we’d expect.

Once the basic simulation was in place, modifications I would add include:
– Variable tree size. The wood density would decide the total cross-sectional area of trees, and you could rather easily vary the radius per tree and keep track of total area so as not to exceed the desired density
– Foliage. Trees (bushes) could have a ‘transmission ratio’, possibly linked to a secondary radius (to discriminate between trunk and leaves). So line of sight could be half-blocked for instance if you were viewing your friend through leaves (as opposed to blocked by a trunk)
– Variable field size. The field is nothing more than a construct to give some constraint to the problem. It would be trivial to instead solve the following: “You and your friend stand in a forest full of trees. What is the percent chance you can see your friend?“

I strongly suspect the results would show a strong proportionality between the magnitude of AB, the wood density and the chance of seeing your friend, and it’s likely an equation could be fitted to allow for a general solution.  It’s tempting to suppose the trivial result would simply equal wood density (ie 50% trees = 50% chance), but my gut tells me it isn’t that simple.

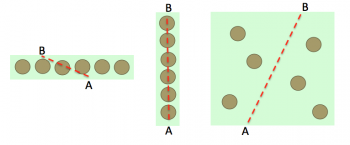
One interesting consideration is the dimension of the field, and how it may affect results. I have mostly ignored it here, but it may be worth considering. Consider the following examples:

Each permutation has 6 trees, but the first two have very narrow fields, both of which will lead to very low chances to see your friend (for random A, B positions). It’s true that the ‘wood density’ varies strongly between the first two the one on the right, and I wonder if that will be enough to correlate the results. In other words, can the exact field dimensions actually be ignored?

So lets return to the general problem, and what has caused me to think about all this: How far can you see in the woods?

It’s a much more interesting problem to imagine, but I think I may save it for another post  🙂

About that clever technique: It occurs to me a completely different way of solving this would be to do it graphically and exploit hardware graphics techniques. For instance, make the trees sprites and draw a vector between A and B and see if there is a collision with a tree. Do this enough times and save the results. The resolution (and I don’t mean computer screen resolution) would be necessarilly less, but maybe this technique – which saves a lot of coding and vector algrebra calculations – could work?

This entry was posted on Thursday, March 12th, 2015 at 9:37 am and is filed under Miscellaneous, Otaku, Puzzles, Tech, The Unknown. You can follow any responses to this entry through the RSS 2.0 feed. Both comments and pings are currently closed.