I’ve been thinking about the Infinite Monkey Theorem, which postulates that an infinite amount of monkeys banging away on keyboards randomly forever would eventually produce the works of Shakespeare. You can read about this in detail here.

I thought to myself, rather than use dirty monkeys to reproduce Shakespeare (which has been attempted), why not use a machine brain? So I turned to an actual honest-to-goodness computer and wrote a simulation.

My machine was the Commodore 64, and I wrote a simple piece of code to randomly generate three letters in order and test to see if they spelled ‘act’, the first word of Hamlet. I was testing the water, so to speak, instead of diving right into a full reproduction of the entire play.

Now it’s fairly simple statistics to calculate that of the 17576 possible three letter words, only one is ‘act’. But I started by looking for words that started with ‘a’ (ie. of the form a–) of which there are 676, and then words starting with ac-, of which there are 26. I timed my result to see if – as expected – each successively correct letter took approximately 26 times as long to generate as the previous.
Here’s my code alongside one example output looking specifically for ‘act’:
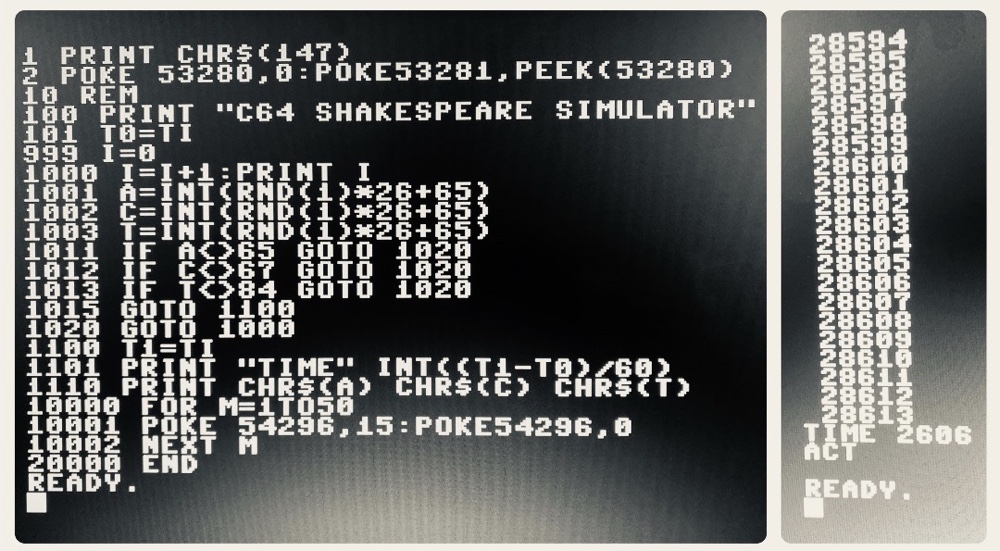
The time is in seconds, and I ran 12 searches each for a– and ac- and 5 (due to the time required) for act. Here are the average times to generate each type of result:
A–: 3 seconds
AC-: 84 seconds
ACT: 2027 seconds
These numbers are close to 26x multiples of each other as expected, and I imagine were I to do enough tests they would converge to that value. From these results we can speculate how long it may take for my C64 to recreate Hamlet…

But first some facts: Hamlet has 132680 letters and 199749 characters in total including spaces and seven punctuation signs. Including these but ignoring case, there are 34 potential candidates for each character and 199749 characters need to be generated. My predictions that follow are based on times equal to 34/26 of those listed above.
The expected (ie. 50% chance) time it would take my C64 to randomly generate Hamlet would be 34^199746 times 1908 seconds which is (approximately) 34^199739 million years. The minimum time is about 1.7 hours ( if it got it right on the first go) and the maximum is of course infinity.
But – given our universe is only less than 14,000 million years old – this means I’m confident in saying my C64 would never randomly generate Hamlet. In fact were I to expand the sim to look for the sequence ‘Act 1’ I would expect the average successful attempt to take about one month. If I extended the sim all the way to the first spoken word – over 100 characters in – I’d expect the Earth would be consumed by the sun before my C64 did it.

Some of you say “that’s just a C64!”, which is primitive compared to the device you’re reading this on. But even if your fancy phone or laptop is a trillion times more powerful, this is nothing compared to a factor of ~10^200k.
It’s pleasant to think of infinite typing apes (or computers) randomly spewing out a work of art, but it would never happen 🙂
(Incidentally and somewhat related; the world is still awaiting the results of B’s testing of this!)













